Die Maxwell-Gleichungen anschaulich erklärt. Folgendes sehr gut gemachtes Video zum Thema Maxwell-Gleichungen habe ich auf YouTube gefunden. Das Video stammt von Jörn Loviscach, der auf seiner Website regelmäßig sehr gut gemachte Videos zur Mathematik und Elektrotechnik veröffentlicht.
Dieses Video zu den Maxwell-Gleichungen ist m.E. einer der Highlights auf seiner Seite.
Die Maxwell-Gleichungen bilden die Grundlage der Elektrotechnik. Die Beschäftigung mit den Maxwell-Gleichungen ist aber nichts für Einsteiger.
Die Inhalte des Videos sind ganz eindeutig Hochschulstoff.
Um das Video zu verstehen sollten man einigermaßen fit im Bereich der partiellen Differentialgleichungen sein.
Meine Empfehlung für Elektrotechniker
Falls Du Dich aber zur Zeit mit den Maxwell-Gleichungen beschäftigst, bzw. beschäftigen musst (die wenigsten Elektrotechniker machen das freiwillig 😉 ) solltest Du Dir das Video unten auf der Seite auf jeden Fall anschauen. Es lohnt sich.
Das elektrische Feld
Wie wirkt das elektrische Feld auf eine Probeladung?
Zu Beginn des Videos wird sehr anschaulich erklärt, wie das elektrische Feld definiert ist und welche Wirkung das elektrische Feld auf eine Probeladung hat.
Das elektrische Feld definiert die Größe und die Richtung einer Kraft auf einer Probeladung in genau diesem elektrischen Feld. Das elektrische Feld ist also genau wie die Kraft auch ein Vektor.
Das magnetische Feld
Im Gegensatz zum elektrischen Feld hat das magnetische Feld keine Kraftwirkung auf ein ruhendes Elektron.
Erst bei der Bewegung der Probeladung wirkt eine magnetische Kraft.
Senkrecht zur Geschwindigkeitsrichtung, dem Geschwindigkeitsvektor, und senkrecht zum Magnetfeld wirkt dann eine Kraft auf die Probeladung.
Die Kraft bildet sich aus dem Produkt der Probeladung und dem Kreuzprodukt aus Geschwindigkeitsvektor und Magnetfeld.
Mit Hilfe der Drei-Finger-Regel, kann man also die Richtung des Kraftvektors bestimmen.
Lorentzkraft im weiteren Sinn
Die Auswirkuing beider Felder, dem elektrischen Feld und dem magnetischen Feld ergibt die Lorentzkraft inm weiteren Sinn.
Also:
F= q (E + v x B)
(wobei F, E, v und B jeweils Vektoren sind)..
Elektrische Ladung und Stromstärke
Desweiteren benötigt man für das Verständnis der Maxwell-Gleichungen weitere Begriffe, die im folgenden definiert werden.
Die elektrische Raumladungsdichte bezeichnet die eingeschlossene Ladung in einem infinitesimal kleinen Volumen.
Für bewegte Ladungen definiert man die elektrische Stromdichte ∂.
Die elektrische Stromdichte bezeichnet die Stromstärke, also die Anzahl der Ladungsträger pro Zeit durch eine infinitesimal kleine Fläche.
Weiter „aufgedröselt“ 😉 ergibt sich, dass die elektrische Stromdichte dem Produkt aus Raumladungsdichte und dem Geschwindigkeitsvektor entspricht.
Kontinuitätsgleichung
Stellt man sich ein kleines Volumen vor, in das Ladungsträger herausfließen, dann müssen diese Ladungsträger nach dem Herausfließen fehlen.
Logisch, oder 😉
Die Änderung der elektrischen Stromdichte nach allen Richtungen, also die Summe der partiellen Ableitungen (nach den einzelnen Richtungen) ∂Jx/∂x + ∂Jy/∂y + ∂Jz/∂z muss gleich der sich in der Zeit geänderten Raumladungsdichte sein.
dJx/dx + dJy/dy + dJz/dz = -∂δ/∂t
dJx/dx + dJy/dy + dJz/dz nennt man div J (Divergenz).
Also lautet dir Kontinuitätsgleichung
div J = -∂δ/∂t
Weniger mathemaisch ausgedrückt bedeutet das, dass Ladungen nicht verloren gehen.
Die vier Maxwell-Gleichungen
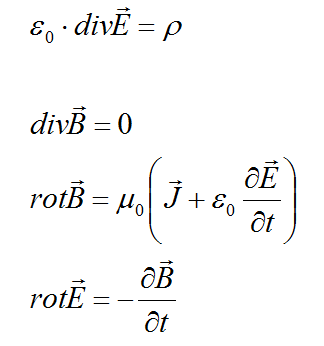
Das Gaußsche Gesetz für elektrische Felder
In der ersten Maxwell-Gleichung betrachtet man die in ein Probevolumen „hinein- und hinausfließende“ elektrische Feldstärke.
Umschließt das Probevolumen positive Ladungsträger fließen mehr Feldlinien hinaus, umschließt das Probevolumen negative Ladungsträger fließen mehr Feldlinien hinein. Die Divergenz des elektrischen Feldes ist also proportional zur Raumladungsdichte.
Das Gaußsche Gesetz für magnetische Felder
Da magnetische Felder keinen Anfang und kein Ende haben, kommt in keinem Punkt magnetische Flussdichte dazu oder geht magnetische Flussdichte verloren.
Es gibt nämlich keine magnetischen Ladungen, bzw. magnetische Monopole.
Die Divergenz von B ist also überall gleich Null.
Das Durchflutungsgesetz
Das Durchflutungsgesetz beschreibt wie elektrische Ströme magnetische Felder erzeugen.
Die Stromdichte erzeugt eine magnetische Flussdichte, die proportional zur Stromdichte ist. Für die magnetische Flussdichte gilt:
rot B ist proportial zu J und zusätzlich (wie im Video gezeigt wird) der zeitlichen Änderung des elektrischen Feldes.
Die Richtung der magnetischen Flussdichte lässt dich aus der „Rechte-Hand-Regel“ bestimmen.
Im Video wird sehr schön am Beispiel einer Kondensatoraufladung gezeigt, dass nicht nur durch den fließenden Strom, sondern auch durch die Änderung des elektrischen Feldes zwischen den Kondensatorplatten ein B-Feld entsteht, das plausibel zum Durchflutungsgesetz ist.
Das Induktionsgesetz
Auch die Änderung des Magnetfeldes hat ein elektrisches Feld zur Folge. Dies wird im Induktionsgesetz beschrieben.
Das Induktionsgesetz lautet rot E = –∂B/∂t
Beispiele zur Anwendung der Maxwell-Gleichungen
Diese vier Maxwell-Gleichen beschreiben vollständig die Zusammenhänge zwischen elektrischen Feldern und magnetischen Feldern und bilden die Grundlage für die Elektrotechnik.
Eigentlich reichen diese vier Maxwell-Gleichungen und der Rest ist nur Ballast. 😉
Nein, im Ernst. Auch ich bin froh, dass man weitere Gleichungen entwickelt hat, die uns Elektrotechnikern das Leben erleichtern.
Wie man aber auch mit den Maxwell-Gleichungen rechnen kann, wird am Ende des Videos gezeigt. Dranbleiben lohnt sich also. 😉
Übungsaufgaben
Allein durch das Lesen bekommt man nur ein grobes Verständnis für die Maxwellschen Gleichungen.
Anwenden kann man diese Gleichungen nur durch entsprechende Übungen anhand von Beispielaufgaben.
Falls Du Dich also schon ein bißchen mit den Maxwellschen Gleichungen auskennst und auf der Suche nach Übungsaufgaben bist, findest Du im nebenstehenden Buch passende Aufgaben mit Lösungsansätzen.
Das Video zu den Maxwell-Gleichungen
Jetzt aber zum Video.
Für alle, die sich mit der theoretischen Elektrotechnik, Systemtheorie oder wie sich das Fach an der Hochschule sonst noch nennt, beschäftigen und sich bereits ein wenig mit partiellen Differentialgleichungen auskennten, lohnt es sich alle Ablenkungen auszuschalten und 50 Minuten lang dem Video zu folgen.




