In vielen Bereichen der Nachrichtentechnik und in der Regelungstechnik werden Systeme daraufhin untersucht, wie sie auf Sinussignale unterschiedlicher Frequenzen reagieren.
Die wenigsten realen Signale sind jedoch keine reinen Sinussignale.
Warum kümmert man sich dann so intensiv um die Sinussignale?
Grund hierfür ist ein Darstellung von Systemen, benannt nach dem französischen Mathematiker Jean-Baptiste-Joseph Fourier.
Hintere den Erkenntnissen von Fourier verbirgt sich viel Mathematik, auf die ich hier nicht tiefer eingehen möchte/kann.
Die zentrale Aussage von Fourier lässt sich aber mit einem Satz vereinfachen.
Nach Fourier lässt sich jedes periodisches Signal aus einer Summer von Sinus- und Cosinus-signalen zusammensetzen.
Fourier für Elektrotechniker
Für uns Elektrotechniker ist diese Aussage von Fourier sehr hilfreich.
Statt unsere Systeme in der Nachrichtentechnik für alle möglichen Signale zu untersuchen hilft es uns, das Verhalten für unterschiedliche Frequenzen von Sinus-Signalen zu beschreiben.
Nach Fourier können wir uns dann auch diesen Sinus-Signalen wieder zusammenbauen.
Auch wenn dies nach Fourier nur für periodische Signale geht und auch wenn wir, wenn wir ein Signal sehr genau aufbauen möchten, unendlich viele Sinus- und Cosinus-Signale addieren müssen, gelten viele Aussagen von Fourier auch, wenn man Vereinfachungen zulässt.
Also, ab und zu man Fünfe gerade sein lassen 😉
Fourierreihe
Jedes periodische Signal lässt sich also nach Fourier durch eine unendliche Summe von Sinus- und Cosinus-Signalen aufbauen.
Interessant dabei ist, dass man nicht alle Frequenzen benötigt, sondern nur die Frequenz des Signals, das man zusammenbauen möchte und die Vielfachen dieser Frequenz.
Die Formel für die Fourierreihe lautet also:
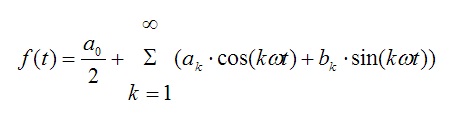
Endliche Summe der Fourierreihe
Wie gesagt, man benötigt zwar nur die Vielfachen den Grundschwingung. Da es davon aber unendlich viele gibt, kommt trotzdem einiges zusammen 😉
Durch eine Approximation mit einer begrenzten Anzahl von Schwingungen erhält man auch schonsehr interessante Ergebnisse.
Die Formal lautet dann also:

Meine Empfehlung für Elektrotechniker
Koeffizienten der der Fourierreihe
Fourier gibt auch an, wie man die Koeffizienten a und b berechnet. Dies kann man mit Hilfe der Integralrechnung tun. Für viele Signalformen gibt es aber auch Tabellen, bzw. Rechenvorschriften im Tabellenbuch.
Fourier in einem Video
Im folgenden Video möchte ich einmal zeigen, wie man Signale mit den Erkenntnissen von Fourier aufbauen kann.
Viel Spaß mit dem Video.




