Wechselstrom

Spannungen und Ströme, die über einen längeren Zeitraum konstante Werte annehmen, heißen Gleichspannung bzw. Gleichstrom.

Im Gegensatz dazu spricht man bei Spannungen bzw. Strömen, die zeitabhängig sind, von Wechsel-, bzw. Mischgrößen. Reine Wechselgrößen, die als keinen Gleichanteil besitzen nennt man Wechselspannung, bzw. Wechselstrom.

Wechselspannungen und Wechselströme könnten hierbei unterschiedliche Kurvenverläufe haben. Wichtige Kurvenverläufe sind beispielsweise Rechteckspannungen, Dreickeckspannungen und sinusförmige Spannungen.

In der Signaltheorie, aber auch in einer wesentlichen Anwendung der Elektrotechnik, der Energietechnik, sind sinusförmige Spannungen und Ströme von besonderer Bedeutung.

Um diese sinusförmigen Verläufe geht es im Folgenden.

Angefangen bei einfachen Wechselstromschaltungen geht es dann um Anwendungen, wie der Energieübertragung und der Nachrichtentechnik.

Wechselsignale werden hier sowohl im Zeitbereich als auch mit Hilfe von Zeigerdiagrammen betrachtet. Die Berechnung mit Hilfe komplexer Zahlen behandele ich dann anschließend.

Bislang sind folgend Artikel erschienen:

Wechselspannung und Wechselstrom an elektrischen Bauteilen

Wie erzeugt man Wechselspannung

Erzeugung einer Wechselspannung durch Differenzieren des magnetischen Flusses

Periodendauer und Frequenz

Effektivwert einer Spannung

Phasenverschiebung

Kapazitive Impedanz (Kondensator)

Induktive Impedanz (Spule)

Wirkleistung und Blindleistung

Wechselstromkreis mit Widerstand und Induktivität

Addition von Spannungen im Zeitbereich

Zeigerdiagramme in der Wechselstromrechnung

Zeigerdiagramme erleichtern das Rechnen mit sinusförmigen Wechselgrößen enorm.
Durch die Umwandlung der Scheitelwerte in Effektivwerte und die Darstellung der Zeiger mit dem entsprechenden Phasenwinkel wird die Berechnung von Wechselstromkreisen sehr vereinfacht.
In dem folgenden Videos geht es darum, was Zeigerdiagramme sind und wie man damit rechnet.

Zeigerdiagramme

Wirkleistung, Blindleistung und Scheinleistung mit Zeigerdiagrammen

Impedanz

Blindleistungskompensation

Spannungserhöhung im Reihenschwingkreis

Spannungsprüfung in der Hausinstallation mit dem DUSPOL

Blindleistungskompensation

In der folgenden Aufgabe, werden die Methoden der Wechselstromrechnung am Beispiel der Blindleistungskompensation für einen Wechselstrommotor angewendet.
Hierfür ist die Gesamtaufgabe in kleine Unteraufgaben aufgeteilt, die dann in kleinen Lösungsvideos erläutert werden.

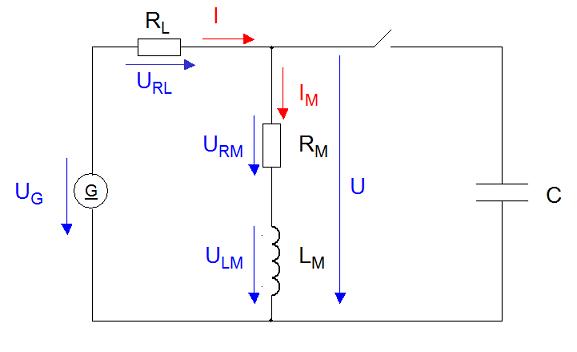
Aufgabe zur Kompensation der Blindleistung für einen Elektromotor

Die Ergebnisse der Aufgabe

Gesamtimpedanz des Motors und Leistungsfaktor

Stromstärke in der Leitung

Spannung U_G, die vom Generator geliefert werden muss

Spannungen U_RM, U_LM, U_RL und U_G im Zeitbereich

Zeigerdiagramm für alle Spannungen

Wirk-, Blind- und Scheinleistung des Motors mit Zeigerdiagramm, Verlustleistung im Leitungswiderstand R_L

Leistungsdiagramm mit der Blindleistung des Kondensators,  Berechnung der benötigten Kapazität des Kondensators

Berechnung der Stromstärke in der Leitung und Zeigerdiagramm

Die Verlustleistung im Leitungswiderstand R_L nach der Kompensation

Weitere Videos zum Thema Wechselstrom

Weitere Videos zum Thema Wechselstrom findest Du unter der Rubrik Komplexe Zahlen.

Mit Hilfe der komplexen Zahlen können auch kompliziertere Aufgaben der Wechselstromrechnung gelöst werden.

Aufwändige Zeigerdiagramme, die mit aufwändigen Rechnungen mit trigonometrischen Funktionen berechnet werden müssten, können mit Hilfe der komplexen Wechselstromrechnung beispielsweise auf sehr einfache Rechenoperationen zurückgeführt werden.

Es lohnt sich also auch, sich mit der komplexen Wechselstromrechnung zu befassen.